五線紙のパンセ｜うなり、快なり～特殊調律の探求 2｜森田泰之進
うなり、快なり～特殊調律の探求 2
An analysis of experimental works for specially tuned pianos in the United States 2
Text by 森田 泰之進 (Yasnoshin MORITA)
2. 3. WTPの構成
ヤング《ウェル・チューンド・ピアノ》（以下WTP）について、ヤング自身がDVDのライナーノーツ(1)で示したところによれば、WTPは9つの部分から構成されている。オクターブ内の12の音が2群に分かれ、各部によってそのどちらか、またはその両方が使われている。ヤングはライナーノーツで2群にそれぞれ「The Opening Chord」「The Magic Chord」と名づけた(2)。このうちセクション1が「The Opening Chord」、セクション3が「The Magic Chord」、セクション4、5、7、8は「The Magic Chord」の変形、セクション2と6は両者間の移行形、セクション9は「The Opening Chord」の変形である。
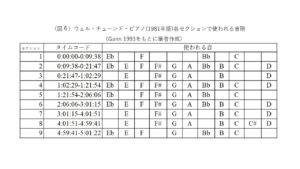ガン(1993)(3)は9つのセクションで使われる音を一覧表化した（図6）。第1セクションでは、Eb、F、Bb、Cの4音であり、周波数比は「8：9：12：14」である。Eb音に対してF音は第9倍音、Bb音は第3倍音、C音は第7倍音にあたり、周波数比は比較的単純である。
9分過ぎからの第2セクションになるとB音とD音、F#音とA音、G音、E音が順に登場し、21分過ぎの第3セクションになるまでに第1セクションの4つの音に代わってE、F#、G、A、B、D音の音階に置き換わる。音律の基音であるEb音が姿を消すが、各音の音程の周波数比は単純で、例えば、63/32で調律されているD音に対する各音の周波数比はEは9/8、Fは7/4、Aは3/2である。第3セクションの音階は第7、8セクションでも現れ、第1、2セクションで使われた音階と対比をなすように扱われる。
ガン（1993）は、各セクションで使われる音を分析したが、具体的に各セクションの中で音はどのように扱われているのか。
各セクションの構成には一定の傾向がみられる。ヤングはほぼどのセクションでも、冒頭で2つの音からなるゆっくりしたテンポの和音をいくつか弾き、その音響を十分聴かせたあと、急速なトレモロや分散和音などに移る。冒頭のゆっくりした和音は、そのセクションで使われる音のいわば「提示部」ともいえるものである。
WTPにおいて、基音Eb音に対するそれぞれの周波数比で単純なものは分母・分子とも1桁、複雑なものは3桁である。これらを使って2音の和音を作る場合、1桁の音どうしを組み合わせれば和音の協和感は高まるのに対し、どちらか一つの音の桁数が2桁、3桁になると、和音のうなりは強くなる。
第1、第2セクションでは分母・分子とも1桁の音が選ばれているのに対し、第3セクションで2桁、3桁が選ばれ、第5、第6セクションでいったん1桁中心に戻った後、第8セクションにかけて再び2桁、3桁が多用される傾向が見られた。第8セクションでは使われる音の大半が3桁になるが、最後の第9セクションで3桁の音は消え、2桁か1桁の単純な周波数比にやや戻る。全体の傾向として、行きつ戻りつしながら、基音Ebに近い音程から縁遠い音程に移行し、最後にEb音と近親音に戻って終わるのである。
(1) La Monte Young The Well-Tuned Piano JUST DREAMS JD002（DVD）（筆者訳） p.18-20
(2) La Monte Young The Well-Tuned Piano JUST DREAMS JD002（DVD）（筆者訳） p.18-20
(3) Gann, 1993 p.143
2. 4. なぜ「7」を選んだか
WTPの音律は純正律のうち純正三度（第5倍音）の代わりに純正七度（第7倍音）を採用し、純正五度とともに音律の基本にしている。一方、素数「5」＝第5倍音（純正三度）が欠落している。ではヤングは、基本倍音の中でなぜ第7倍音に注目したのか。
仮にうなりを音楽制作の重要な目的にするとしたら、7、11、13などの素数に着目するであろうことは容易に想像できる。第3、第5倍音は純正律で使われており、これらを使っただけでは個性的な音響を生み出す可能性は限られるからである。もし7より数の大きい素数を使えば、他の数と掛け合わせたときの数が大きくなりやすい。音響的にいえば、うなりを含んだ音響を生みやすいのである。ヤングが当初、第31倍音を一部導入していた（前述）ことを考えれば、少なくとも図2の縦軸として第7倍音の代わりに第11倍音や第13倍音の適用を考えた可能性は十分にある。
ではヤングはなぜ、第11、13倍音を使わなかったのか。
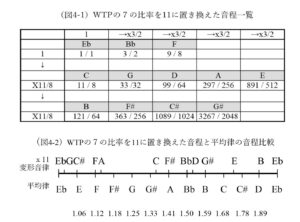
筆者は、図2のWTPの音律表のうち、縦軸「第7倍音」を第11倍音、ならびに第13倍音にそれぞれ書き換え（図4-1、図5-1）、さらにこれを図3に倣って平均律との比較表にあてはめてみた（図4-2、図5-2）。まず第11倍音の音律について見ると、EbとG、FとA、BbとDの間隔、ならびにGとC#、CとF#、DとG#の間隔は均等だが、ヤングが採用した第7倍音の音律が一定の音程パターンを形成するのと比べ、全体として規則性が希薄であり、主要音と色付け音の序列を付けづらい印象である（図4-2）。
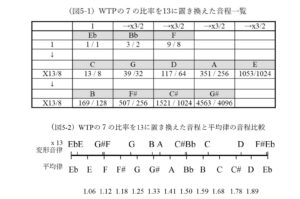
さらに第13倍音の音律ではG#とF、C#とBb、F#とEbの間隔が均等だが、前述第11倍音の音律と比べてさらに規則性が希薄になる。またこれらの音程のペアは、ヤングの第7倍音の音律における主要音E、Bb、Fと周辺の色付け音の関係に比べ、2音間の音程差が非常に狭い。このためピアノ調律に適用した場合、近接した2音が米国のカントリー音楽に使われるホンキートンクピアノのように、少し調子の狂った同一音程と認知される可能性がある。うなりを含んでいる点で目的を達しているが、音程が近接し過ぎて逆に音律の独自性を打ち出しにくい（図5-2）。
加えて、2音を鳴らした際の「差音」がどの程度効果的に鳴るか、という点もある。差音とは、高さの異なる2つの音が同時に響くときに発生する、両音の振動数差にあたる振動数をもつ音をいう。例えば400Hzと300Hzの2音の場合、その差にあたる100Hzが差音であり、その周波数が人間の可聴領域であれば差音として聴取される。聴取者は演奏音を一定時間注意深く聴くことにより差音に気が付きやすくなる。ヤングは差音を、演奏された2音から発生する、実際には存在しない「欠落した基本音」(4)と呼び、創作上重視していた。
筆者がWTPの音源を数度聴取したところ、急速なトレモロや分散和音の場面で非常にゆっくりした低音がわずかに聴きとれるようになった。鳴らす2音の周波数値が近い場合、差音の周波数値は小さく、つまりピッチはより低くなる。ピアノの最低音Aの周波数は27.5Hzであるから、差音の周波数値がこのあたりを下回ると音として認識されづらくなる代わりに、「ワンワンワン」という周期的なうなり音となって聴取されるようになる。さらに周波数値が小さくなると、うなりの周期音として聴取できる範囲さえ下回り、聴取者に認識されづらくなる。
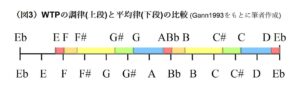
逆に差が大きくなり、かつ整数比になるような2音、例えば協和感が高い純正律で調律した場合、差音はよりはっきり聞こえる。つまり、聴取者が差音をはっきり聴取できる2音の周波数の間隔は、広すぎずかつ狭すぎず、一定の範囲に収まるのが効果的であり、ヤングが、差音を創出しやすい音律として、第11や第13ではなく第7倍音を軸の一つとした音律（図3）を選んだと見るのが自然である。
まとめると、ヤングにとって望ましい音律とは、（1）音階の中に（E、Bb、Fのような）主要音と、これらに近くうなりまたは差音を発生させる「色付け」音が設定できること、（2）「色付け」音は主要音に近接しすぎず、うなり音程または差音がはっきり聴取できるよう主要音との間で一定の音程差を維持すること――であり、第7倍音を最適な縦軸として選んだと推察できる。
(4) La Monte Young The Well-Tuned Piano JUST DREAMS JD002（DVD）（筆者訳） p.5
2. 5. ヤングにとっての音響認知と音律
そもそもヤングはなぜ、倍音やうなりに興味を持ったのか。藤枝（2007）は本作品に至るヤングの音響体験との関係を指摘している。
ヤングは、故郷アイダホ州の大平原に張られた送電線に風が吹き抜けるときに発生する持続音をしばしば聞いていた。風向きや風速の変化によって倍音を微妙に変化させる音を通じて、ヤングは「ドローンのような引き伸ばされた音と倍音による抑揚に興味を持った」(5)。また、亀を飼っていたヤングは、亀の水槽の空気用モーターの持続音（60Hz）をヒントに、正確に音高を生みだす正弦波発振器を何台か使った倍音列による持続音に聞き入り、「声をその持続する響きに同化させることによって、純正音程がもつ音響的な特性を身体のなかにしみ込ませた」(6)。
こうした音響体験を経たヤングはやがて、独自の音楽創作の理論的根拠を音響心理学に求めるようになる。WTPのDVDの解説文で、ヤング自身が言及している。
「単純な分子や分母の比は、複雑な比よりも短時間で周期の複合波形を生成する。逆に、分子と分母が非常に大きく、合成波形の1回の完全な周期が人間の一生よりも長く続くような、合理的な周波数比によって表される周期を想像してみてほしい。…その全体を聴くこともできないような遅い周期性の音程を理解したり分析したりすることは望めない。…東西の伝統的な音楽は、2、3、5の素数に限定されたシステムの上に広大なレパートリーを構築できることを示してきたが、より複雑な整数比の認識と理解を体系的に発展させることも可能であることが、次第に明らかになりつつある」(7)。つまり、純正律よりもっと複雑な分数比の音程による音楽を聴取者が楽しむ場合、「遅い周期性」を認知するのに時間がかかるため、深く味わうためには長時間聴く必要がある、とヤングは説いているのである。純正律では単純すぎるが、あまりに複雑過ぎる分数比でも具合が悪い。第7倍音を縦軸とする音律は、こうした諸条件を満たす点でヤングには頃合いの良い音律だったのである。
ヤングはその音律を表現するための条件として、ピアノの重要性を説く。「有理数を使ったシステムは、古代の古典的な音楽体系のモードにまつわる感覚の幅と深さを取り戻し、さらに新たな未踏の感覚の領域へと進むための無限の可能性を与える。有理数に基づく音程は、繰り返し正確に調律できる唯一の音程であるため、繰り返し聴いてもまったく同じに聴こえる可能性がある唯一の音程なのである。複雑さの閾値が徐々に拡大する中で、有理数の音程によって生み出される感情が、認識され記憶される可能性を持ち、その結果、強い感情的衝撃をもたらすのはこのためである」(8)。微妙な音程のコントロールには、調律の安定が必要である。これを考えたとき、ヴァイオリンやサクソフォンなどの管弦楽器よりも、調律を事前にある程度固定できるピアノのほうが有利であることに間接的に触れている。
ヤングはこのように、単に自らの音楽的志向だけでなく、数学的な思考と科学の知見を背景に、聴取者が聴覚を研ぎ澄ませるための時間を計算し、またピアノという楽器の特性を踏まえて創作したのである。
(5) 藤枝, 2007 p.157
(6) 藤枝, 2007 p.158
(7) La Monte Young The Well-Tuned Piano JUST DREAMS JD002（DVD）ライナーノート（筆者訳） p.5-6
(8) La Monte Young The Well-Tuned Piano JUST DREAMS JD002（DVD）ライナーノート（筆者訳） p.5
2. 6. ガムラン、インド音楽との関係
ヤングの音律設計を考えるとき、もうひとつ重要なのは民族音楽との関係である。米国では西海岸を中心に1950年代後半以降、作曲家ルー・ハリソン（Lou Harrison, 1917-2003）を中心に若い音楽家たちによるガムラン音楽のサークルが数多く生まれた。ハリソンは自作のガムラン楽器を交えた作曲、演奏に加え、聴覚体験により伝承されてきたインドネシア各地の「ガムランの多様な音律の世界を、純正律という方法によって明らかにしようとした」(9)。
ガムランの典型的音階のひとつであるスレンドロの調律は、オクターブをおおむね5分割した5音音階といわれている。それぞれの音程は全音（長二度）のように聞こえるが、ハリソンによれば、どの音を音律の基準とするかによって8/7、7/6、9/8、32/27など「いくつかの全音が存在」(10)しており、これらはいずれも純正律に基づいているという。ハリソンは自作の《ピアノとジャワ・ガムランのための協奏曲 Concerto for Piano with Javanese Gamelan》でも、この音律原理を使っている。
ある特定の音程に純正律を適用した場合、複数の周波数比がありうることにヤングも着目した。前述の通りWTPの音律（図3）において、E音とF音、A音とBb音、D音とEb音はそれぞれ近接している。例えば基音Eb音を1とした時の周波数比はE音が567/512、F音が9/8（図2）、小数で表すとそれぞれ1.10742、1.125であり、演奏を聴くと調律のズレた同一の音として聴取されやすい。この点、ハリソンを通じたガムラン音楽からの影響を見ることができる。
加えて、ヤングは純正三度音程を作り出す第5倍音を避けている点で、ガムランと共通する。前述の通り、ガムランの調律法の基礎となる分数比において、2、3、7とその倍数は登場するが、5の倍数は避けられている。ヤングが3、7の倍数を基礎にWTPの調律を設定（図2）したことを考えれば、彼はガムランなど民族音楽を参考に「純正三度を生み出す5という存在を排除することによって、西欧音楽の響きから抜けだし、そして5の代わりに7という素数を用いて独自の音律を編みだした」(11)と言える。
ヤングの音律にはインド民族音楽の影響もみられる。前述の通りWTPは数度改訂されているが、1973年稿では1964年稿に比べて「より大規模で精巧なテーマに基づいた即興作品へ変貌」(12)した。1970年代前半、ヤングはインド民族音楽の声楽家プラン・ナート（Pran Nath, 1918-1996）(13)に数年間師事していた。ナートの歌唱スタイルは「明瞭で表現力豊かなイントネーションを重視し、演奏全体を通して加速を最小限に抑えたゆっくりとしたテンポを好み、速く複雑なリズムやシンコペーションを避け」(14)る。ヤングはその絶妙な音程感覚のコントロールと即興演奏の魅力に惹かれ、WTP改訂稿に取り入れたのである。WTPにおいて、テンポが緩いこと、その中で微妙な音程を聴かせること、時折現れる即興的な音の運びからは、ナートをはじめとするインド民族音楽の影響がうかがえる。
(9) 藤枝, 2007, p.146
(10) 藤枝, 2007, p.147
(11) 藤枝, 2007, p.163
(12) Welch, 1999（筆者訳） p.183
(13) プラン・ナート Pran Nath (1918-1996) インドの声楽家、作曲家。デリー大学で教鞭をとったあと、1970年に初めて欧米で演奏し、ヒンドゥスターニー古典音楽の声楽の伝統を米国に広めた。(La Monte Young 2014 Pandit Pran Nath Grove Music Online, 筆者訳 Oxford University Press.)
(14) Welch, 1999（筆者訳） p.183
3. テリー・ライリー《ハープ・オブ・ニュー・アルビオン》
3. 1. 作品について
《ハープ・オブ・ニュー・アルビオン》（以下HNA）のCDのライナーノーツによれば、「ニュー・アルビオン」とは現在サンフランシスコ湾と呼ばれているノヴァ・アルビオンである。この地には、16世紀後半にニュー・アルビオンの海岸に置き去りにされたハープをアメリカ先住民の医者が発見し、崖の上に置いたところ、西風が吹いて弦が鳴り、温度と湿度の上下による調律の変化により絶えず音色が変化した、という伝説がある。ライリーはこれにインスピレーションを受け、純正律のピアノをハープに見立てて作曲した。
3. 2. ライリーの使った音律
HNAにおける音律は、純正三度（5/4）、純正五度（3/2）を軸にした純正律である（図7）。基音C#音を中心に、純正三度上のF音、純正三度下のA音そしてそれぞれの純正五度上または下の音から音程を決めていく。この音律では、C#音を主音とした調性音楽では、うなりを感じさせない協和した和音として響くのである。
ところが、この作品において10楽章のうちC#音を主音とする楽章はない。各楽章の主音と支配的音程、さらに支配的音程内の主音とその他の音の周波数比を図8にまとめたが、冒頭の第1、第2楽章はA#を主音とする短調（嬰イ短調）、すなわちC#（嬰ハ長調）の平行調である。これが後半の楽章になるとC#音との関係が希薄な音に移っていく。第3、第5、第6、第8楽章はC#音の半音上のDを主音とし、支配的音程である短三度のD－Fは純正律であれば6/5となるべきところ、75/64という、うなり感の強い音程が支配的な音響になっている。B#音を主音とする第7、第9楽章では、調性音楽の基本となる長三度、四度音程にさえ数字の大きい分数が出現し、特に第7楽章のB#音とG音の五度音程は、純正律の場合3/2となるべきところ、 1024/675となり、分母、分子の数字は最大となる。その後、数字は第10楽章に向かって徐々に縮小していくが、一桁の整数まで戻ることはなく、うなり音を含んだ響きのまま曲を閉じる。
3. 3. HNAの構成
では各楽章の中で、構成音はどのように使われ、移行していくのか。各楽章の構成音の移行を、C#音を基準とした周波数比をみると、第1楽章では15/8であるC音以外は1桁、第2楽章では分母、分子とも1桁の音のみであるが、第3楽章以降、第10楽章まで分母、分子とも2桁の音が1回以上登場する。さらにその出現パターンを見ると、ひとつの楽章の中で比較的協和感の高い和音と、うなりの強い和音がゆきつ戻りつ登場する傾向が表れている。
また曲の中で支配的な音程の提示の方法にも特徴がみられる。例えば第1楽章はA#音を基礎とする自然短音階が基本であり、ゆっくりとしたコラールである。純正律が含む不協和音程は少々出てくる程度であり、聴取していても音律の特殊性はさほど感じない。しかし第2楽章では、冒頭から18/25の特殊な音程の主音A#と増四度上のE音が連打される。これはうなり音程を聴き慣れない聴取者にはなじみにくいであろう。こうした連打や急速な分散和音が後半に向かって随所に登場し、純正律がはらむ特殊音程を強調するのである。
ここで注目すべき点がそれぞれ五度の関係にあるE―B音と、C－G音の音程である。第10楽章でB―Eの音程（E―Bの転回形）が出てくるが、ここでの音程は純正律の完全五度ではなく54/40（B－Eの場合40/54）であり、強いうなりを含んでいる。
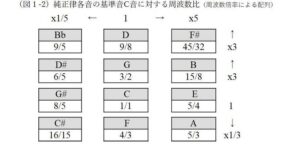これは意図的に設定されたと思われる。ライリーの音律チャート（図7）を標準的な純正律のチャート（図1）と比較してみよう。C#音を基音とする純正律ならば本来9/5（チャート左上）にあるべきB音と、 45/32（チャート右上）にあるべきG音は、ライリーのチャートではそれぞれチャート下部に置かれ、それぞれ16/9、64/45の分数が割り当てられている。これはそれぞれ五度関係にあるE―B音、C―G音間で完全五度から外れたうなり音程が発生することを意図して、切り離されたと考えられる。
まとめると、HNAにおいては、比較的単純な周波数比の音の組み合わせから終盤へ向けて周波数比の複雑な組み合わせへ漸次移行するが、その過程で、楽章によって周波数比の複雑なものと単純なものを行き来する部分がみられる。ライリーは、複雑な周波数比を実現するため、一部の音程でうなりが出やすいよう標準的な純正律の音程を操作して独自の音律決定を行っていることがわかる。
ここまで、ヤングとライリーの特殊音律を概観したが、では彼らがピアノの差音やうなり音を使って喚起しようとした感覚や精神世界とはどのようなものか。また彼らが音律を体系化し、差音やうなり音の周波数比を明確に定めた理由は何か。第3回でこれらを考察する。
参考文献：
Kyle Gann, 1993, La Monte Young’s The Well-Tuned Piano, Perspectives of New Music vol. 31, No. 1. Winter. p.134-162
Kyle Gann, 2009, The Outer Edge of Consonance Sound and Light : La Monte Young and Marian Zazeela, Bucknell University Press.
Kyle Gann, 2019, The Arithmetic of Listening: Tuning Theory and History for the Impractical Musician, University of Illinois Press.
Allison Welch, 1999, Meetings along the Edge: Svara and Tāla in American Minimal Music, American Music. 17, University of Illinois Press. p.179–199
藤枝守, 2007『響きの考古学』（平凡社）
参考音源とライナーノーツ：
La Monte Young The Well-Tuned Piano Gramavision, 18-8701-2（CD）
La Monte Young The Well-Tuned Piano JUST DREAMS JD002（DVD）
Terry Riley The Harp of New Albion celestial harmonies, 14018-2（CD）
(2025/12/15)
―――――――――――――――
【プロフィール】
森田 泰之進 Yasnoshin MORITA
作曲を松平頼暁、Frédéric Durieuxの各氏に師事。2009年ヴァレンティノ・ブッキ賞(イタリア)、2013、2023年ISCM世界音楽の日々(ウイーン、南アフリカ)入選、2017年ISCM世界音楽の日々(ヴァンクーヴァー)招待作曲家。日本現代音楽協会理事。日本作曲家協議会、オーケストラ・プロジェクト会員。
【ウェブサイトや作品視聴】
YouTube: https://www.youtube.com/@Yasnoshin
Website: https://www.jscm.net/morita_yasunoshin/
Instagram: https://www.instagram.com/yasnoshin/
Spotify : https://open.spotify.com/track/6uenN83IGyG9MsYZVz7pQB
CD : Kumi Uchimoto – 24 Preludes From Japan – Stradivarius – STR 37089
Takashi Matsudaira – Utakata = うたかた – ENZO Recordings – EZCD-10021
【公演情報】
★森田泰之進《音信》（おとづれ）
愛知室内オーケストラ第95回定期演奏会
2026年2月28日［土］開場:13:15 開演:14:00
東海市芸術劇場（愛知・名鉄太田川駅下車）大ホール
https://ac-orchestra.com/news/20251007/
★森田泰之進《音輪》（おんりん）2本の笙と各種音楽再生機器のための
作曲家グループ邦楽2010「音ト遊ブ」
2026年4月19日［日］午後1時30分開演
としま区民センター（東京・池袋） 小ホール
★森田泰之進《速驚曲第3番》
「コントラバス百万石」
2026年5月16日［土］午後3時開演
KMアートホール（東京・幡ヶ谷）
