五線紙のパンセ｜うなり、快なり～特殊調律の探求　１｜森田 泰之進

うなり、快なり～特殊調律の探求　１
An analysis of experimental works for specially tuned pianos in the United States 1

Text by 森田 泰之進 (Yasnoshin MORITA)

和音における「協和」とは何か。音響学的には「小さな整数比となる異なる周波数の音波の共鳴振動を意味」⁽¹⁾し、心理学的には「2つあるいはそれ以上の音の調和的響きを意味する。この場合、響きには『粗々しさがなく』、諸音間の緊張も緩和されている」。しかし「協和」にはもうひとつ重要な条件がある。それは聞き取った聴取者がその和音を「快い音」と感じるかどうか、である。ある音程が協和か不協和かは聴取者の音楽聴取経験、聴取者が属する文化や社会環境などにより変化しうるものであり、「快」か否かという個人の「美的な嗜好」の判断でもある。
協和、不協和の基準は時代により変化してきた。紀元前5世紀のピタゴラス学派で「協和音」は五度とオクターブとその派生音程だったが、中世以降長三度などもこれに準じるものと位置づけられるようになった。長三和音などの中に「美」を見いだすようになったのである。
その後「協和」の概念はさらに変化する。
20世紀に入ると、従来常識とされていた12平均律以外の、例えば純正律に由来する微分音を加えた音律が提案された。アメリカの作曲家ハリー・パーチ（Harry Partch, 1901-1974）は、1オクターブの中に43の音が入る「拡張された純正律（extended just intonation）」の音階を考案した。ある基音に対して短三度、長三度、完全四度、完全五度の周波数比が単純な分数になる音程はうなりのない音程だが、別の音に対してはうなりが発生する場合が多い。パーチは、オクターブ内各音に対して極力うなりを排除した音程を用意するため、微妙に音高が違うたくさんの音を設けたのである。
一方、アメリカの作曲家ルー・ハリソン (Lou Harrison、1917-2003）は、ガムランへの傾倒の中で純正律のもつ音高の不揃いに興味をもち、不均等な音程が旋律を特微づけ、魅力あるものにすることに気づき、この組織化を試みた。うなり和音の中に価値を見つけたのである。
こうした先駆的取り組みを受けて登場したのが、作曲家・鍵盤楽器奏者であるラ・モンテ・ヤング（La Monte Young, 1935‐　）とテリー・ライリー（Terry Riley, 1935‐　）である。彼らは純正律を基礎にしたピアノ独奏作品において、純正律が想定しない、強いうなり音が発生する組み合わせの和音を用いた。しかも一般聴衆が「調律の外れた和音」と感じうるうなり音程の調律に厳密な体系化が行われた。彼らはうなり音程から音楽的魅力を引き出そうとしたのである。
本論では特に断りのない限り、便宜的に19世紀ロマン派に代表される西洋クラシック音楽の美の基準を念頭に「協和」という用語を使うことにする。ただヤングやライリーが「うなり音」の中に美を見いだしていることを考えれば、彼らにとってうなり音は「協和音」ということになろう。
本論は、両作曲家のピアノ即興の代表作であるヤング《ウェル・チューンド・ピアノ　The Well-Tuned Piano》（1964）、ライリー《ハープ・オブ・ニュー・アルビオン　The Harp of New Albion》（1984）における調律法を通じて、「拡張された協和音」としてのうなり音程の仕掛けを概観し、彼らが独自の調律法に込めた意図を考察する。

(1) Claude V. Palisca and Brian C.J. Moore 2001 Consonance　Grove Music Online, 筆者訳 Oxford University Press.

1．　音律探究者としてのヤングとライリー

1. 1.　ミニマル・ミュージックの一潮流としての音律探究

ラ・モンテ・ヤング（La Monte Young, 1935‐　）とテリー・ライリー（Terry Riley, 1935‐　）はともに戦後アメリカの現代音楽の潮流「ミニマル・ミュージック」の中心人物であり、音律に着目し、ピアノに各自固有の調律法を適用した。
ミニマル・ミュージックとは「1960年代前半からアメリカで顕著になった、作曲素材の範囲の縮小を急進的に目指した音楽」⁽²⁾を指し、単純なフレーズや音素材が長時間継続または繰り返される音楽である。結果として聴取者は、その際に生じる音響の微細な差異や変化に関心を向けることになる。ヤング、ライリーに加え、スティーブ・ライヒ（Steve Reich, 1936‐　）、フィリップ・グラス（Philip Glass, 1937‐　）を加えた計4人がミニマル・ミュージック初期の中心人物とされる。
ライヒやグラスは短く軽快な音型パターンを長時間繰り返し、そのパターンを徐々に変形させるのが特徴である。一方ヤングとライリーはリズムによる推進力が希薄なかわりに、音数を極力絞り込み、独自の音律が生む周期的波動をじっくり聴取者に聴かせ、聴取者の耳を演奏音の微細な変化に向けさせる点で共通している。
彼らがピアノ調律の際に使ったのが、ルネサンス時代から使われてきた純正律による調律である。西洋音楽では長らく倍音関係を背景に、極力うなりのない和音が重視され、楽器調律法もこれを意識しつつ発展してきた。これに対し、ヤングやライリーの純正律の使い方はうなりを多く含む和音を重視する傾向であり、本論で取り上げる2作品はその傾向を明確に示している。
これらの作品におけるヤングとライリーはともに近代音楽の調律の前提である平均律に批判的な立場である。平均律は、ごくわずかなうなりをはらみつつ12すべての調で一定の和声の協和を実現し、古典派以降の音楽表現の幅を飛躍的に広げた。つまり平均律を採用している限り、どのような音選びをしても聴衆に「うなり音」とはっきり認識されうる音程の発生はほぼ排除されるのである。これに対しヤングとライリーによる純正律を基礎にした調律法では、選ぶ音の組み合わせによって一般聴取者が「協和」と認識しうる和音と「うなり音」と認識しうる和音の差がみられる。ヤングの《ウェル・チューンド・ピアノ》が演奏時間約5時間、ライリーの《ハープ・オブ・ニュー・アルビオン》は約1時間50分の即興演奏であるが、複数の音の連打や同音反復などを通じて、うなりを含む和音の音響に注意を向けるよう聴取者を誘導する。彼らはうなり音程を長時間聴かせることで、聴衆にある心理的状態が生まれることを期待したのである。

(2) Keith Potter 2019 Minimalism (USA) Grove Music Online, 筆者訳 Oxford University Press.

1. 2.　ヤング、ライリーの活動と倍音音律に関わる作品

このうちヤングの作風は3つの期間に分けることができる。第1期の1950年代後半、ヤングはUCLAでレナード・スタイン（Leonard Stein, 1916–2004）に作曲を学んだ。スタインは当時現代音楽の最先端であった十二音技法の創始者アーノルド・シェーンベルク（Arnold Schoenberg, 1874-1951）の同僚である。その後ヤングは、1959年に「偶然性の音楽」で有名なジョン・ケージ（John Cage, 1912-1992）に見出され、ノイズや身振りも取り入れた音楽に取り組んだ。これが第2期である。この後、音律を創作の柱に据える第3期に移行するが、ここには第2期の経験が反映している。ケージは、聴覚的に知覚可能なあらゆる音響を音楽的素材として導入し音楽的素材の領域を拡張した。ヤングも「拡張」という点で似ているが、ケージがコンサート会場の雑音などに興味を惹かれるのに対し、ヤングはむしろある楽器の一つの持続音に聴取者の注意を向けさせ、単音であっても倍音に基づく内部構造を持ち、多様な音を知覚できることを発見した。任意の楽器のための《コンポジション1960 #7、Composition 1960 #7》（1960）では、完全五度を構成するB音とF#音を「極力長く伸ばす」⁽³⁾という指示がある。続いて室内楽曲《ザ・セカンド・ドリーム・オブ・ザ・ハイテンション・ライン・ステップ・ダウン・トランスフォーマー　The Second Dream of the High-Tension Line Step down Transformer》（1962）では、低いC音を基音に、その3オクターブ上のG、C、C#、D音に対してそれぞれ第36、35、34、24倍音を割り振っている⁽⁴⁾。ここでは音程の組織化は4つの音にとどまっているが、2年後の《ウェル・チューンド・ピアノ》では音律の組織化が12音すべてに広がっている。
一方ライリーは、ドイツの作曲家カールハインツ・シュトックハウゼン（Karlheinz Stockhausen、1928‐2007）の影響を受けたのち、1959年ごろからヤングとともに即興演奏を始めた。ライリーは同年生まれのヤングを師と仰いでおり、ヤングに倣う形で音律への関心を深めた。本論文の研究対象である《ハープ・オブ・ニュー・アルビオン》はヤングに献呈されている。
この時期、音律に着目したライリーの主な作品としては、室内オーケストラを想定した不定人数のための《インC　In C》（1964）があげられる。純正律ではないが、基音Cに対し、倍音列を連想させるE、F#、G、A、Bb、B音が多く使われ、その後の純正律志向の原点を見ることができる。このほかいずれも純正律を用いた、純正律電子オルガンのための《Shri Camel》(1980)、ピアノ独奏のための《ハープ・オブ・ニュー・アルビオン Harp of New Albion》(1984)、サクソフォン四重奏のための《チャンティング・ザ・ライト・オブ・フォーサイト　Chanting the Light of Foresight》（1987）が知られている。2020年代に入り、ライリーはアメリカから日本へ活動の拠点を移し、2025年現在、演奏活動をはじめ、自然や宇宙のムードを実体験するインド古典音楽「ラーガ」を教えている。

(3) Wim Mertens, 1988, American Minimal Music, Kahn & Averill, p.26
(4) William Duckworth & Richard Fleming, eds, 1996, Sound and Light: La Monte Young and Marian Zazeela. Lewisburg: Bucknell University Press, p.143–144

1. 3.　 両作曲家にとっての純正律

図1-1

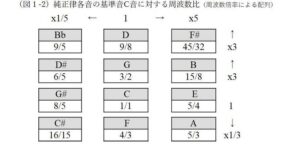
ヤングとライリーが音律構造を決める際の原点となったのは純正律である。これは基音の振動数に対し整数倍の振動数をもつ倍音音程のうち、第3、第5倍音をもとにオクターブ内の12音の音律を体系化したものである（図1-1）。特にライリーの《ハープ・オブ・ニュー・アルビオン》にはこれに近い音律が使われている。

図1-2

純正律では、基音に対して純正五度（第3倍音の1オクターブ下）、純正三度（第5倍音の2オクターブ下）をまず定め、音階の骨格となる音（C-major＝ハ長調の場合、C、E、G）を作る。これらの音をもとに他の音の音程を決めていく。例えば基音をCとした時、周波数比3/1の音を第3倍音といい、純正律ではこの1オクターブ下、つまり周波数比3/2にあたる音をG音と定める（図1‐2中央列）。同じ手順でG音に対して周波数比3/2であるD音を導き出す。また3/1の逆数である周波数比1/3の音をFとする。　これで基音Cの5度圏の近接音であるD、G、F音（図1-2中央列）が導かれる。次に各音の周波数比5/1にあたる音からそれぞれ長三度上の音（図1-2右列）、また1/5にあたる音から長三度下の音（図1-2左列）を導き出す。
図1では、基音Cを中心に、縦軸を上にたどると周波数は3倍、下方向は1/3倍、右方向は5倍、左方向は1/5倍となる。例えば、基音Cから上方向の第3倍音をG音、右方向第5倍音をE音とするのだが、倍音のままでは基音とそれぞれ1～2オクターブも離れてしまい、1オクターブ内で完結させる「音階」の範囲から外れてしまう。このため、前述の通り分数値の分母または分子に2またはその乗数をかけることで、周波数比の値1～2以内、つまり1オクターブに収まるよう操作している。ヤングやライリーの音律も、この手順で各音の音高を決定している。
純正律の特徴は、基音Cやそれに近い音階を使った和音が、うなりがなく美しく響く点にある。複数の音は、周波数比が単純になればなるほど音波の共振が高まり、協和感の高い和音として聴取されやすくなる。純正律ではB、F#、C#以外は分母、分子とも1桁の分数であり、基音Cとその周辺の音、特にC-E-G、またはG-B-Dのような長三和音は協和感が高くなるのである。
このように、純正律は基音に対する倍音をもとにした音階である。和声は美しいが、基音の調とその近親調以外に転調した場合、和音はうなりが目立ち、協和感が乏しくなる。これは純正律において1オクターブの中の12音それぞれの音程（周波数の差）が不均等であるためである。そのため純正律は自由な転調が前提となっている現在の音楽で一般的ではない。
ヤング、ライリーの音楽を「純正律を使った作品」と表現すると、協和感が高い音響を志向した曲、という印象を持たれる可能性があるが、これは誤解である。彼らは純正律をそれぞれ改変した独自の音律を採用しており、むしろうなり音の波動に注目させ、一般に「不快」と受け取られることが多いうなり音の中に、「快」または「美」を見つけ出そうと試みている。

2. ラ・モンテ・ヤング《ウェル・チューンド・ピアノ》

2. 1. 作品について

《ウェル・チューンド・ピアノ》（以下WTP）は1964年に初演されたヤングによるピアノ即興演奏作品であり、楽譜は存在しない。ヤングの主な関心は音楽の形式ではなくピアノの調律そのものだったのである。このため、従来のクラシック音楽の楽曲分析のような楽譜をもとにした形式、音符の分析と異なり、もとになっている音律の分析が楽曲研究の中心となる。
ヤングは1950年代からサクソフォンの演奏活動を展開する一方、純正律への関心を高めた。しかし、サクソフォンは管の穴の位置が固定されているため自由に音律を変えられる楽器とは言いがたい。いくつかの管楽器で試した後、彼は管楽器をあきらめ、1964年ごろから純正律のピアノに取り組み始め、同年ニューヨークで開かれた私的なライブで、45分間の即興演奏を披露した。これがWTPである。
この後、1973年、1981年の演奏の際、調律が一部変更されている。演奏時間は大幅に拡大され、CDが残っている1981年稿の演奏は約5時間である。

2. 2. ヤングの使った音律

WTP（1981年稿）の音律の基礎は純正律であり、基音に対し周波数比「3/1」「7/1」にあたる第3倍音と第7倍音を軸としている。以下、カイル・ガン（Kyle Gann 1955- ）によるWTPの音高解析をもとに論じる。

図2

ガンの分析（1993）⁽⁵⁾を要約すると、WTPの音階では、まず基音（Eb音）に対して周波数比3/2（第3倍音の１オクターブ下＝純正五度）のBb音、また音階上では六度上にあたり基音と周波数比7/4（第7倍音の2オクターブ下＝純正七度）となるC音の３つの音が柱となる（図2）。さらにBb音、C音の周波数を3/2倍（純正五度＝図2の縦軸）または7/4倍（純正七度＝図2の横軸）した音から12の音を導く。
これを純正律（図1-2）と比較する。純正律では、3、5の倍数と同時に、3、5の逆数（1/3、1/5）も使われている。基音Cと周辺音間の周波数比は比較的単純な分数であり、和音として鳴らした際の協和感が高い。これに対し、ヤングの音律では倍数のみで逆数は使われておらず、図では基音（Eb）から下および右方向に伸びていく。このため、基音から遠く離れたG#音は分母・分子とも4桁の分数、A、E、C# 、F#は3桁の分数になっている。これらの音と基音、またはこれらの音のうち複数の音を和音として鳴らすと、多くの人にはうなりの強い音響として認識されやすくなる。純正律と比較して、分母・分子の桁数が多い分、振動がずれている時間が長くなるからである。

図3

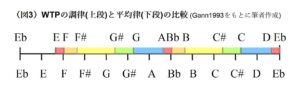
この音律のもうひとつの特徴は、音階のうち2カ所で音高が逆転していることである（図3、Gann1993の図に筆者が着色）。
G音は21/16、G#音は1323/1024であるが、これを、平均律の半音をひと目盛りにしてならべるとG#音のほうが半音近く低くなる（図3）。同様にC音とC#音の関係でもC#音のほうが低い。ヤングの音階と平均律音階とを比較すると、音階の割り振りの不均等性が際立つ。Eb、F、Bbの周辺に、1～2個の音が集中しているのがわかる。これらの音は近接しているため、同時に鳴らすと、歪んだ調律による一種のクラスター音として聴取されやすい。
さらにオクターブ中の音高分布にはあるパターンを見ることができる。
同じ周波数比になっている箇所を同色で色分け（図3）すると、音群「A、Bb、B、C#、C」と「E、F、F#、G#、G」が同じ音程パターンを繰り返し、両者の構成音はそれぞれ純正の完全5度の関係にあることがわかる。一方、音群内の個別の音に着目すると「E、F、F#」「A、Bb、B」「D、Eb」は音程が近接し、聴取者には、若干調弦の外れた同音と聴き取られうる。
上記の1981年稿WTPでは、音律の軸は第7倍音（7/4）と第3倍音（3/2）の2本だが、ガン（1993）によれば、1964年稿ではこれにもうひとつ別の軸「第31倍音（31/16）」が設定されており、12音のうちC# 音が31/16、G#音がC#音の完全五度（3/2）上の93/64、E音はそのさらに完全五度上の279/256に調律された。1973年稿ではE音の調律が少し上がり、最終稿と同じA音の完全五度上に変更され、さらに1981年稿でC#音とG# 音も現行の縦横2つの軸内に収められたため、第31倍音の軸は消滅した⁽⁶⁾。
第3、第7に比べ、聴取者に協和音程として認識されにくいと思われる第31倍音の音程を、一時的にせよヤングはなぜ選んだのか。ガン（1993）は「ヤングの作品でドローン（持続低音）を基礎にした正弦波の音律の多くは、ドローンの1オクターブ上よりわずかに高いか低いピッチ（例えば31/16、63/32、および129/128）を中心としている」⁽⁷⁾と指摘しており、ヤングが音階内で主要音とそうでない音を分け、主要音に少しだけ外れた高さの音を加えてうなりを発生させ、音に独特の色付けをしようとしていたことを示唆している。
歴史上の多くの音楽家たちは倍音を基礎に音階や和音の「協和」が「美」であると認識し、音楽を生み出し続けてきた。これに対しヤングの目指したのは、わずかなうなり音に色付けられた音響の中に「美」を見出す音楽であると言える。
ではヤングが、第5、第11倍音などではなく第7倍音を選んだのはなぜか、またライリー作品における音律構造については次回考察する。

(5) Gann, 1993（筆者訳） p.136
(6) Gann, 1993（筆者訳） p.141
(7) Gann, 1993（筆者訳） p.141

引用文献：
Claude V. Palisca and Brian C.J. Moore 2001, Consonance  Grove Music Online, 筆者訳 Oxford University Press.
Keith Potter 2019, Minimalism (USA) Grove Music Online, 筆者訳 Oxford University Press.
Kyle Gann, 1993, La Monte Young’s The Well-Tuned Piano, Perspectives of New Music vol. 31, No. 1. Winter. p.134-162
Wim Mertens, 1988, American Minimal Music, Kahn & Averill, p.26
William Duckworth & Richard Fleming, eds, 1996, Sound and Light: La Monte Young and Marian Zazeela. Lewisburg: Bucknell University Press, p.143–144

―――――――――――――――
【プロフィール】
森田 泰之進 Yasnoshin MORITA
作曲を松平頼暁、Frédéric Durieuxの各氏に師事。2009年ヴァレンティノ・ブッキ賞(イタリア)、2013、2023年ISCM世界音楽の日々(ウイーン、南アフリカ)入選、2017年ISCM世界音楽の日々(ヴァンクーヴァー)招待作曲家。日本現代音楽協会理事。日本作曲家協議会、オーケストラ・プロジェクト会員。

【ウェブサイトや作品視聴】
YouTube: https://www.youtube.com/@Yasnoshin
Website: https://www.jscm.net/morita_yasunoshin/
Instagram: https://www.instagram.com/yasnoshin/
Spotify : https://open.spotify.com/track/6uenN83IGyG9MsYZVz7pQB
CD : Kumi Uchimoto – 24 Preludes From Japan – Stradivarius – STR 37089
Takashi Matsudaira – Utakata = うたかた – ENZO Recordings – EZCD-10021

【公演情報】
★森田泰之進《音信》（おとづれ）
愛知室内オーケストラ第95回定期演奏会
2026年2月28日［土］開場:13:15 開演:14:00
東海市芸術劇場（愛知・名鉄太田川駅下車）大ホール
https://ac-orchestra.com/news/20251007/

★森田泰之進《音輪》（おんりん）2本の笙と各種音楽再生機器のための
作曲家グループ邦楽2010「音ト遊ブ」
2026年4月19日［日］開演時間未定
としま区民センター（東京・池袋）　小ホール